Pág. 202 Santillana Base y altura de triángulos
Aprende:
La base de un triángulo es uno cualquiera de sus lados, por lo tanto, un triángulo tiene 3 bases.
La base de un triángulo es uno cualquiera de sus lados, por lo tanto, un triángulo tiene 3 bases.
La altura de un triángulo es un segmento perpendicular a la base (o a su prolongación), trazado desde el vértice opuesto a esa base. De este modo, un triángulo tiene 3 alturas.
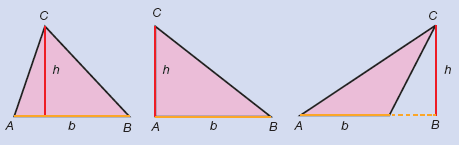
Fíjate bien en los siguientes triángulos. En cada uno de ellos está pintada la base AB de color naranja. También son bases los lados BC y AC.
La altura correspondiente a la base AB está trazada de color rojo.
Recuerda que la altura parte del vértice opuesto a la base (en este caso, desde el vértice C) y es perpendicular a la base (en este caso, AB) o a su prolongación.
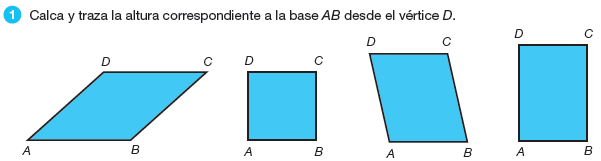
Resolver -> Pág. 202 (nº 1)
Resolver -> Pág. 202 (nº 2)
Resolver -> Pág. 202 (nº 3)
Pág. 203 Santillana Base y altura de paralelogramos
Recuerda:
Los paralelogramos son cuadriláteros que tienen lados paralelos dos a dos.
Paralelogramos ➜ cuadrado, rectángulo, rombo y romboide
Aprende:
La base de un paralelogramo es uno cualquiera de sus lados, por lo tanto, un paralelogramo tiene 4 bases.
La base de un paralelogramo es uno cualquiera de sus lados, por lo tanto, un paralelogramo tiene 4 bases.
La altura de un paralelogramo es un segmento perpendicular a la base (o a su prolongación), trazado desde el vértice opuesto a esa base. De este modo, un paralelogramo tiene 4 alturas.
Fíjate bien en los siguientes paralelogramos. En cada uno de ellos está pintada la base AB de color naranja, que es uno de los lados (el lado b). También son bases, los lados BC, CD y AD.
La altura correspondiente a la base AB está trazada de color rojo. Recuerda que la altura es un segmento perpendicular a la base o a su prolongación, y uno de sus extremos es uno de los vértices opuestos a ella (en estos casos puede ser el vértice C o D).
Resolver -> Pág. 203 (nº 1)
Muy importante:
Área sería la cantidad de espacio que hay dentro de los límites de un objeto plano, como un rectángulo, cuadrado, triángulo o un círculo.
Este espacio se mide en unidades cuadradas (km², hm², dam², m², dm², cm², mm²).
Para resolver los ejercicios donde tengas que calcular áreas, debes utilizar la altura que se corresponde con su base, es decir, la altura que es perpendicular a esa base.
Ahora debes aprender muy bien las fórmulas de las áreas de los polígonos (cuadrado, rectángulo, triángulo); y también del círculo.
Además, debes fijarte muy bien para aprender a descomponer figuras planas, en otras conocidas, para hallar sus áreas.
Es fundamental que en los problemas de áreas:
- dibujes la figura
- escribas su fórmula
- y des la solución en unidades cuadradas.
¡Vamos a comenzar!
Pág. 204 Santillana Áreas del rectángulo y del cuadrado
Presta mucha atención:
Aprende
El área del rectángulo es el producto de su base por su altura. ➔ Área del rectángulo = b x h
Aprende
El área de un cuadrado es su lado elevado al cuadrado. ➔ Área del cuadrado = lado²
Resolver -> Pág. 204 (nº 1)
Resolver -> Pág. 204 (nº 2)
Resolver -> Pág. 204 (nº 3)
Pág. 205 Santillana Área del triángulo
Fíjate bien:
De toda esta explicación se deduce, que el área de un triángulo es la mitad del área del rectángulo que lo contiene. La fórmula queda de la siguiente forma:
Aprende
El área del triángulo es el producto de la base por la altura, dividido entre dos. ➔
Resolver -> Pág. 205 (nº 1)
Resolver -> Pág. 205 (Creatividad)
Pág. 206 El número 𝝅 y la longitud de la circunferencia
𝝅 ⟶ Es una letra griega.
Esta letra la utilizamos en la medida de la longitud de la circunferencia y se llama
número pi.
Este número lo obtenemos al dividir la longitud de una circunferencia entre su diámetro.
El valor del número pi (𝝅) es aproximadamente 3,14 (y no tenemos que ponerle ninguna
unidad detrás).
Presta mucha atención: en este apartado vamos a calcular longitudes (líneas), por lo tanto, los resultados no debemos expresarlos en unidades cuadradas (porque no vamos a hablar de superficies).
Para medir longitudes, utilizamos unidades lineales: km, hm, dam, m, dm, cm y mm.
Vamos a hablar de circunferencias. Recuerda que una circunferencia es la línea que bordea el círculo (es una línea curva cerrada, cuyos puntos se encuentran a la misma distancia del centro).
Fíjate bien:
Aprende
La longitud de la circunferencia es igual al producto de 3,14 por su diámetro. ➔ Longitud de la circunferencia = 𝝅 x d = 𝝅 x 2 x r
Resolver -> Pág. 206 (nº 1)
Resolver -> Pág. 206 (nº 3)
Pág. 207 Santillana Área del círculo
Volvemos otra vez al área ➜ Recuerda utilizar unidades cuadradas.
Recuerda que el círculo es la superficie interior a la circunferencia.
Presta atención:
Aprende
El área del círculo es igual al producto de 3,14 por su radio al cuadrado. ➔ Área del círculo = 𝝅 x r²
Resolver -> Pág. 207 (nº 1)
Resolver -> Pág. 207 (nº 2)
Resolver -> Pág. 207 (Pensamiento)
Pág. 208 Santillana Área de figuras planas
¡Presta atención! ➜ Para calcular el área de una figura plana, hay que:
- descomponerla primero (en otras figuras cuyas áreas sepamos calcular)
- y sumar después las áreas de esas figuras.
En el siguiente dibujo, se quiere calcular el área del parque. Para ello, se ha descompuesto en un cuadrado y un rectángulo. El área del parque será igual a la suma de las dos áreas.
Recuerda que el área debemos expresarla en unidades cuadradas.
Fíjate bien:
Resolver -> Pág. 208 (nº 1)
Figura 1:
Figura 2:
¡Cuidado! ➜ En este ejercicio debes calcular el área de la zona coloreada. Para ello, calcula el área de la figura mayor y luego debes restarle el área de la zona blanca.
Resolver -> Pág. 209 (nº 3)
Figura 1:
Pista:
Puedes descomponer la figura en un rectángulo y un semicírculo.
Rectángulo à base = b = 4 cm altura = h = 2,5 cm
Semicírculo à radio = r = 1 cm
Figura 2:
Pista:
Puedes descomponer la figura en un círculo, un rectángulo y un triángulo.
Círculo à radio = r = 1 cm
Rectángulo à base = b = 5 cm altura = h = 2 cm
Triángulo à base = b = 1 cm altura = h = 2 cm
Resolver -> Pág. 209 (nº 4)
