PARALELOGRAMOS
Resolver -> Pág. 184 (nº 1)
nº. 1 Escribe en tu cuaderno cuántas bases tienen los triángulos y los paralelogramos.
Los triángulos tienen 3 bases y los paralelogramos tienen 4.
Resolver -> Pág. 184 (nº 2)
Alturas correspondientes a las bases AB en cada triángulo:
¿En qué triángulo coincide la altura con uno de sus lados? En el triángulo amarillo.
Clasifícalo según sus ángulos. Es un triángulo rectángulo.
¿En qué triángulo has prolongado la base para trazar la altura? En el triángulo naranja.
Clasifícalo según sus ángulos. Es un triángulo obtusángulo.
¿En qué triángulo has dibujado la altura en su interior? En el triángulo rosa.
Clasifícalo según sus ángulos. Es un triángulo acutángulo.
Resolver -> Pág. 185 (nº 3)
Alturas correspondientes a las bases AB en cada paralelogramo, desde el vértice D:
¿En qué paralelogramos coincide la altura con uno de sus lados? En el cuadrado y en el rectángulo coinciden.
¿En cuál has prolongado la base para trazar la altura? La base se prolonga en la tercera figura (romboide).
¿Desde qué otro vértice puedes trazar la altura a la base AB? Se puede trazar otra altura correspondiente a la base AB desde el vértice C. En este caso, habría que prolongar la base en la primera figura (romboide).
Resolver -> Pág. 185 (nº 4):
- Traza un triángulo ABC cuyos lados midan 4 cm, 3 cm y 5 cm. ¿Cuánto miden las tres bases? Las tres bases miden 4 cm, 3 cm y 5 cm respectivamente.
- Traza un triángulo DEF cuyos lados midan 3 cm, 3 cm y 5 cm. ¿Cuánto miden las tres bases? Las tres bases miden 3 cm, 3 cm y 5 cm respectivamente.
Ahora empezamos a trabajar con problemas de áreas.
Recuerda:
Recuerda:
- Aprender muy bien las fórmulas de las áreas y escribirlas en los problemas.
- Dibujar la figura.
- Y dar la solución en unidades cuadradas.
Pág. 186 ÁREA DEL RECTÁNGULO Y DEL CUADRADO
Resolver -> Pág. 186 (nº 1)
Rectángulo lila → A= b x h = 4 x 3 = 12 cm²
Rectángulo naranja → A = b x h = 8 x 2 = 16 cm²
Cuadrado (amarillo) → A = lado² = 4 x 4 = 16 cm²
Resolver -> Pág. 186 (nº 2)
Explicación 1er. apartado
Rectángulo → A= b x h = 30 x 20 = 600 cm²
El área del rectángulo es 600 cm²
Explicación 2º apartado
Cuadrado → A = lado² = 50 x 50 = 2.500 cm²
El área del cuadrado es 2.500 cm²
Explicación 3er. apartado
Recuerda la pista → El ancho (altura)
sería un tercio del largo, es decir:
altura = 12 : 3 = 4 metros
Rectángulo → A= b x h = 12 x 4 = 48 m² El área de la parcela rectángular es 48 m²
Explicación 4º apartado
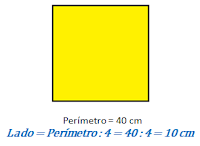
Recuerda que, aunque no te demos la medida del lado, lo puedes calcular porque sabes que el perímetro es la suma de los lados de la figura.
El área del marco cuadrado es 100 cm²
Resolver -> Pág. 186 (nº 3)
Cuadrado verde → A = lado² = 2 x 2 = 4 cm²
Mirando el dibujo vemos que, el lado del cuadrado mayor (2 cm) es el doble que el lado del cuadrado menor (1 cm).
Calculando las áreas vemos que, el área del cuadrado mayor (4 cm²) no es el doble que el área del cuadrado menor (1 cm²). Es el cuádruple.
Pág. 187 ÁREA DEL ROMBO
Resolver -> Pág. 187 (nº 1)
Recuerda la fórmula del área del rombo ➜
Rombo verde → Diagonal mayor = 4 cm
Diagonal menor = 2 cm
Rombo rosa → Diagonal mayor = 5 cm
Diagonal menor = 2,4 cm
El área del rombo rosa es 6 cm²
Resolver -> Pág. 187 (nº 2)
Explicación 1er. apartado
Datos
Diagonal mayor = 12 cm
Diagonal menor = 10 cm
Explicación 2º apartado
Datos
Diagonal menor = 8 cm
Diagonal mayor = 15 cm
Explicación 3er. apartado
Datos
Diagonal mayor y menor son iguales
Medida = 30 cm
¡Cuidado! ➜ Aunque en este apartado nos preguntan por el área de un rombo, en los datos nos dicen que las dos diagonales son iguales, por lo tanto, realmente se trata de un cuadrado, pero no podemos hallar su área con la fórmula del cuadrado porque no conocemos la medida del lado.
Explicación 4º apartado
Datos
Diagonal menor = 6 cm
Diagonal mayor el doble que la menor → 6 x 2 = 12 cm
Pág. 188 ÁREA DEL ROMBOIDE
¡Cuidado! ➜ Fíjate bien en la altura del romboide.
Recuerda que debe ser perpendicular a la base.
Recuerda que debe ser perpendicular a la base.
Resolver -> Pág. 188 (nº 1)
Área del romboide verde = b x h = 2 x 3 = 6 cm²
Área del romboide azul = b x h = 4 x 1,5 = 6 cm²
Área del romboide rosa = b x h = 3 x 2 = 6 cm²
Área del romboide amarillo = b x h = 2 x 2,5 = 5 cm²
Resolver -> Pág. 188 (nº 2)
Romboide B → Área = b x h = 9 x 4 = 36 cm²
Romboide C → Área = b x h = 10 x 4,8 = 48 cm²
Romboide D → Área = b x h = 5 x 12,4 = 62 cm²
¿Qué romboides de los anteriores tienen la misma área? Los romboides A y C.
Dos romboides con distintas bases y alturas, ¿pueden tener la misma área? Dos romboides sí pueden tener la misma área, aunque tengan diferentes bases y alturas (queda demostrado en el ejercicio).
Resolver -> Pág. 188 (nº 3)
El área del prado sí es el doble que el área de la parcela.
Área (parcela) = b x h = 100 x 60 = 6.000 m²
Área (prado) = b x h = 100 x 120 = 12.000 m²
Pág. 189 ÁREA DEL TRIÁNGULO
Recuerda➜ El área del triángulo es el producto de la base por la altura, dividido entre dos. ➔
Resolver -> Pág. 189 (nº 1)
Triángulo azul → base = 4 cm altura = 1,5 cm
Triángulo naranja → base = 2 cm altura = 2 cm
Triángulo rojo → base = 2 cm altura = 3 cm
Recuerda: en el triángulo rojo hay que dibujar su
altura (que debe ser perpendicular a la base). ➜
Triángulo rosa → base = 4 cm altura = 2,5 cm
Resolver -> Pág. 189 (nº 2)
Explicación 1er. apartado
Explicación 2º apartado
base = 4 cm altura = base + 12 = 4 + 12 = 16 cm
Explicación 3er. apartado
Explicación 4º apartado
Resolver -> Pág. 189 ➜ PENSAMIENTO
Los dos triángulos (naranja y verde) tienen las mismas base y alturas. Las bases están superpuestas y la altura de cada triángulo es igual a 2 cm.
Tienen igual área, por tener iguales la base y la altura.
Pág. 190 ÁREA DE POLÍGONOS REGULARES
Recuerda➜ El área de un polígono regular es el producto de su perímetro por su apotema dividido entre dos. ➔
Resolver -> Pág. 190 (nº 1)
Hexágono ➜ Área = 6 x 20 = 120 m²
Octógono ➜ Área = 8 x 20 = 160 m²
Resolver -> Pág. 190 (nº 2)
Pág. 191 ÁREA DEL CÍRCULO
Recuerda ➜El área del círculo es el producto del número 𝜋 por su radio al cuadrado. ➔
Área del círculo = 𝜋 x r² = 3,14 x r²
Resolver -> Pág. 191 (nº 1)
¡Cuidado! ➜ Para hallar la fórmula del círculo verde, recuerda que no puedes utilizar el diámetro. Nos hace falta el radio, por lo tanto, radio = diámetro : 2 = 12 : 2 = 6 cm
Resolver -> Pág. 191 (nº 2)
- Área del círculo rojo = 𝜋 x r² = 3,14 x 3² = 3,14 x 3 x 3 = 3,14 x 9 = 28,26 cm²
¡Cuidado! ➜ Para hallar la fórmula del círculo verde, recuerda que no puedes utilizar el diámetro. Nos hace falta el radio, por lo tanto, radio = diámetro : 2 = 12 : 2 = 6 cm
- Área del círculo verde = 𝜋 x r² = 3,14 x 6² = 3,14 x 6 x 6 = 3,14 x 36 = 113,04 cm²
- El radio del círculo mayor es 6 cm
- El radio del círculo mayor es el doble que el radio del círculo menor.
- El área del círculo mayor no es el doble que el área del círculo menor.
Resolver -> Pág. 191 (nº 2)
Explicación 1er. apartado
Área del círculo = 𝜋 x r² = 3,14 x 5² = 3,14 x 5 x 5 = 3,14 x 25 = 78,5 cm²
Explicación 2º apartado
radio = diámetro : 2 = 4 : 2 = 2 m
Área del círculo = 𝜋 x r² = 3,14 x 2² = 3,14 x 2 x 2 = 3,14 x 4 = 12,56 m²
Explicación 3er. apartado
Área del círculo = 𝜋 x r² = 3,14 x 30² = 3,14 x 30 x 30 = 3,14 x 900 = 2.826 cm²
Explicación 4º apartado
Área del círculo = 𝜋 x r² = 3,14 x 14² = 3,14 x 14 x 14 = 3,14 x 196 = 615,44 cm²
Explicación 5º apartado
radio = diámetro : 2 = 200 : 2 = 100 m
Área del círculo = 𝜋 x r² = 3,14 x 100² = 3,14 x 100 x 100 = 3,14 x 10.000 = 31.400 m²
Explicación 6º apartado
radio = diámetro : 2 = 300 : 2 = 150 m
Área del círculo = 𝜋 x r² = 3,14 x 150² = 3,14 x 150 x 150 = 3,14 x 22.500 = 70.650 m²
Resolver -> Pág. 191 ➜ PENSAMIENTO:
¿Cómo puedes calcular el área de un semicírculo? Es el área del círculo completo, dividido entre 2.
¿Por qué crees que no se estudia ninguna fórmula para calcularla? R.L.
¿Y el área de un cuarto de círculo? Es el área del círculo completo, dividido entre 4.
Aunque las áreas no las habíamos pedido, te dejo aquí la forma de hallarla, por si quieres pensar un poquito más. 😉
Área del semicírculo = (𝜋 x r²): 2 = (3,14 x 2,5²) : 2 = (3,14 x 2,5 x 2,5) : 2 = (3,14 x 6,25) : 2 =
= 19,625 : 2 = 9,8125 cm²
Área del cuarto de círculo = (𝜋 x r²): 4 = (3,14 x 2²) : 4 = (3,14 x 2 x 2) : 4 = (3,14 x 4) : 4 =
= 12,56 : 4 = 3,14 cm²
Pág. 192 ÁREA DE FIGURAS PLANAS
¡Recuerda! --> Para calcular el área de una figura plana, hay que:
- descomponerla primero (en otras figuras cuyas áreas sepamos calcular)
- y sumar después las áreas de esas figuras.
Resolver -> Pág. 192 (nº 1)
- El área de la zona roja es el área del círculo menos el área del cuadrado.
- El radio del círculo mide 12 m.
- El lado del cuadrado mide 10 m.
- Área de la zona roja = 452,16 - 100 = 352,16 m²
Resolver -> Pág. 193 (nº 2)
Figura verde
Su área sería: área del rectángulo menos área del rombo
¡Atención! ➝ Nos dan el largo del rectángulo (base), que se corresponde con la diagonal mayor del rombo. Tenemos también el ancho (altura) del rectángulo, que se corresponde con la diagonal menor del rombo.
Área del rectángulo ➝ A = b x h = 38 x 20 = 760 m²
Área de la figura verde ➝ A = 760 - 380 = 380 m² ➝ El área de la figura verde es 380 m²
Figura morada
Su área sería: área del semicírculo más área del triángulo isósceles.
Área del semicírculo = (𝜋 x r²): 2 = (3,14 x 10²) : 2 = (3,14 x 10 x 10) : 2 = (3,14 x 100) : 2 =
= 314 : 2 = 157 m²
Área de la figura morada ➝ A = 157 + 230 = 387 m² ➝ El área de la figura morada es 387 m²
Resolver -> Pág. 193 (nº 3) En este ejercicio, para hallar el área de las figuras, básate en las siguientes medidas:
¡Cuidado con las figuras rosa y marrón! → a la superficie coloreada debes restarle la superficie blanca.
Figura rosa
Su área sería: área del círculo menos área del romboide
Área de la figura rosa ➝ A = 12,56 - 3 = 9,56 cm² ➝ El área de la figura rosa es 9,56 cm²
Figura roja
Su área sería: área del círculo más área del rectángulo
Área del círculo = 𝜋 x r² = 3,14 x 1² = 3,14 x 1 x 1 = 3,14 x 1 = 3,14 cm²
Área del rectángulo = b x h = 4 x 2 = 8 cm²
Área de la figura roja ➝ A = 3,14 + 8 = 11,14 cm² ➝ El área de la figura roja es 11,14 cm²
Figura marrón
Su área sería: área del triángulo más área del cuadrado menos área del círculo
Área del cuadrado = lado² = 4 x 4 = 16 cm²
Área del círculo = 𝜋 x r² = 3,14 x 2² = 3,14 x 2 x 2 = 3,14 x 4 = 12,56 cm²
Área de la figura marrón ➝ A = 6 + 16 - 12,56 = 9,44 cm² ➝
El área de la figura marrón es 9.44 cm²
Figura amarilla
Su área sería: dos veces el área del triángulo más área del rectángulo
Área del rectángulo = b x h = 3 x 4 = 12 cm²
Área de la figura amarilla ➝ A = 2 x 3 + 12 = 18 cm² ➝ El área de la figura amarilla es 18 cm²
Figura azul
Su área sería: área del semicírculo más área del cuadrado grande + área del cuadrado pequeño
= 3,14 : 2 = 1,57 m²
Área del cuadrado grande = lado² = 4 x 4 = 16 cm²
Área del cuadrado pequeño = lado² = 2 x 2 = 4 cm²
Área de la figura azul ➝ A = 1,57 + 16 + 4 = 21,57 cm² ➝ El área de la figura azul es 21,57 cm²
Figura morada
Su área sería: área del triángulo más área del romboide
Área del romboide = b x h = 4 x 2 = 8 cm²
Área de la figura morada ➝ A = 6 + 8 = 14 cm² ➝ El área de la figura morada es 14 cm²
